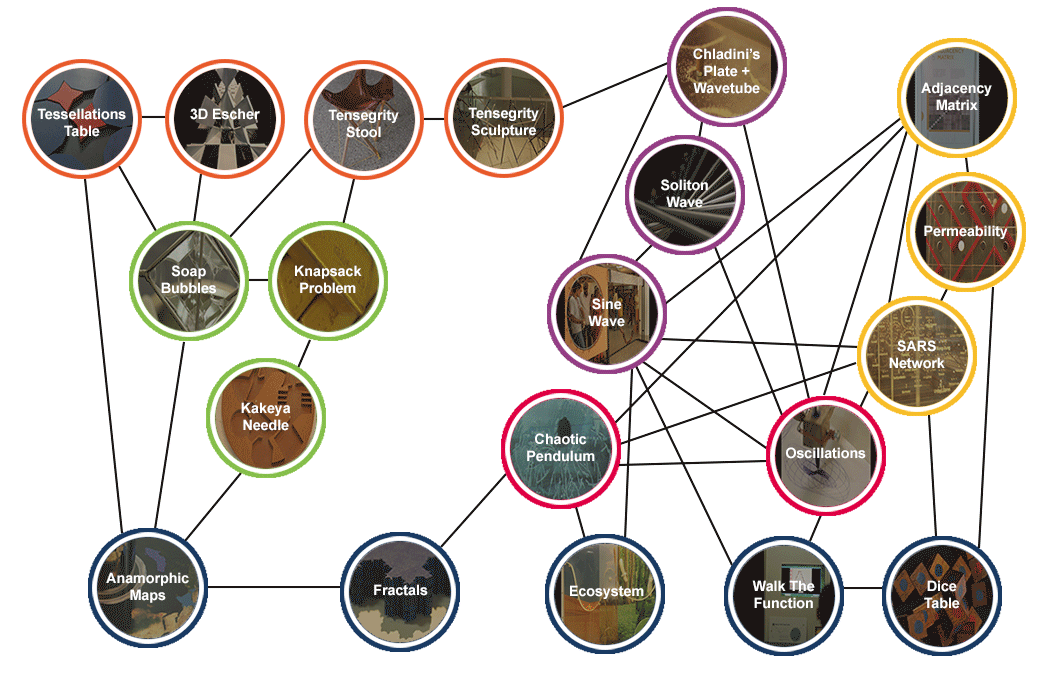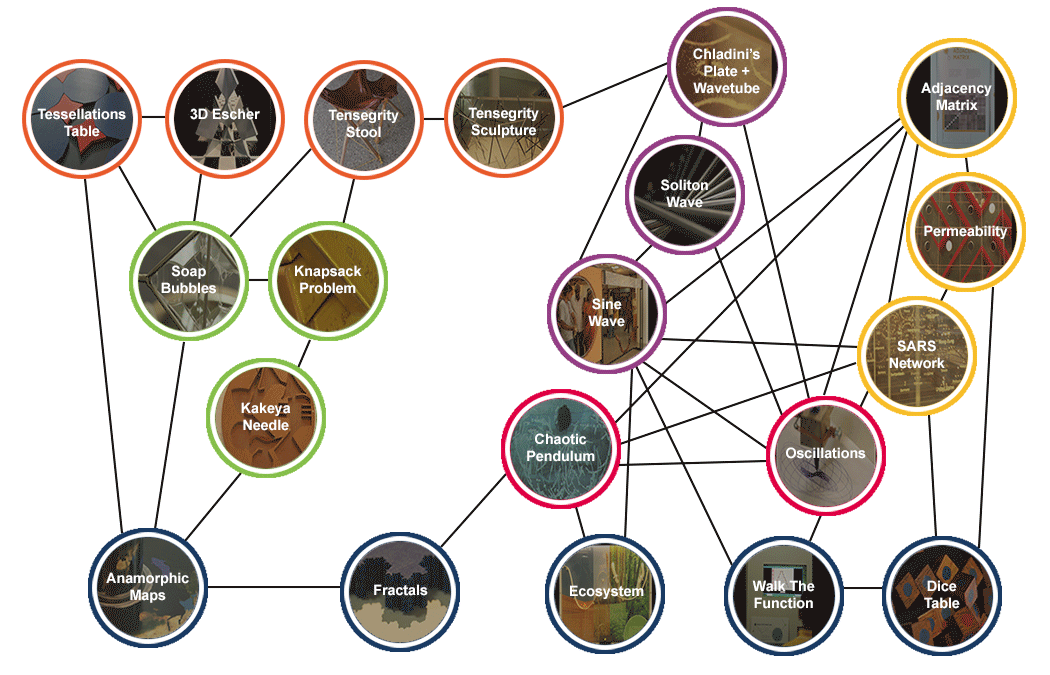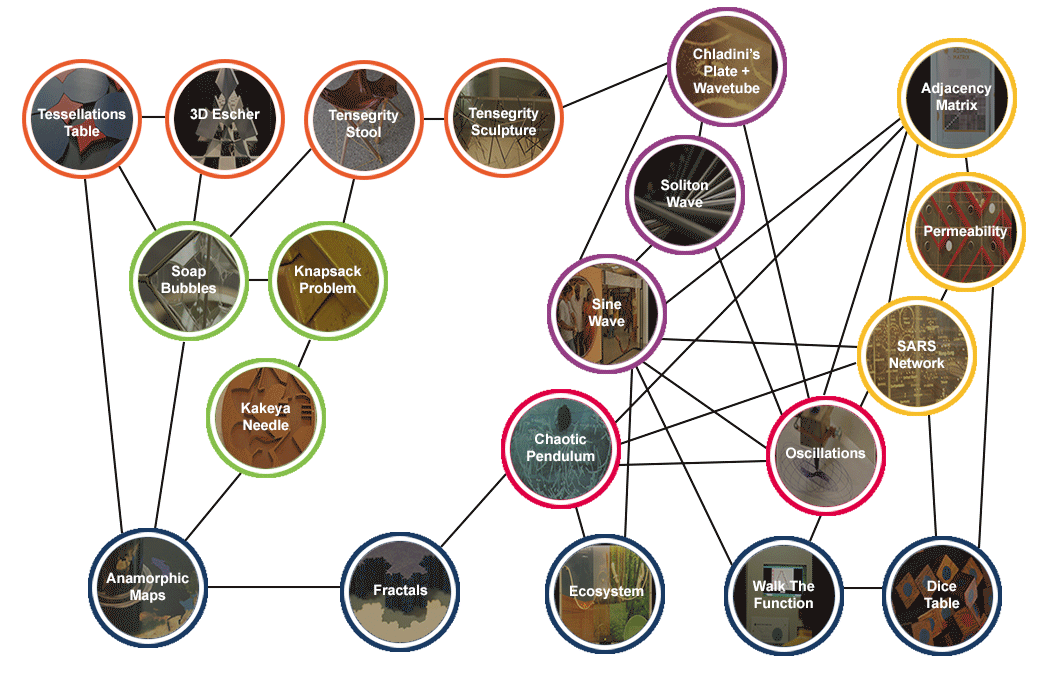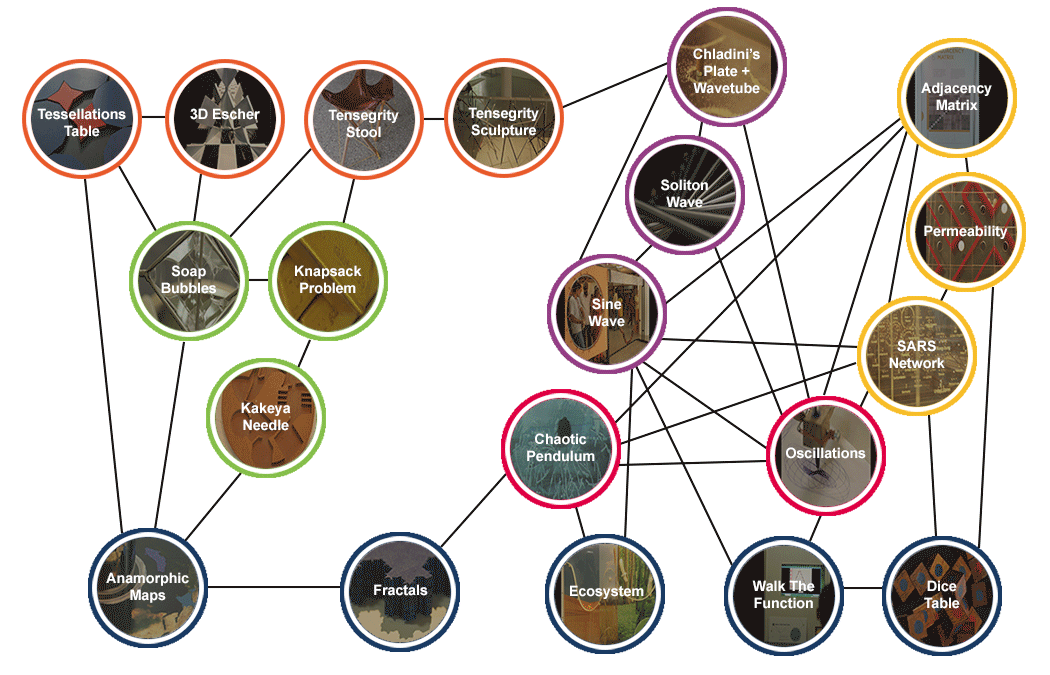
Welcome to the Network Graph
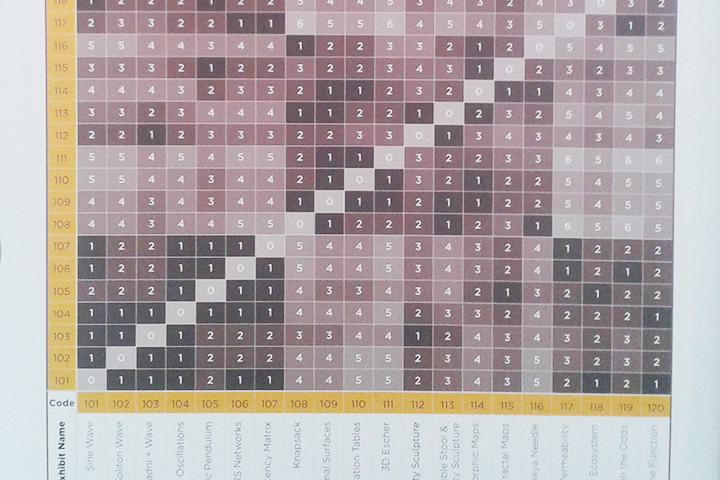
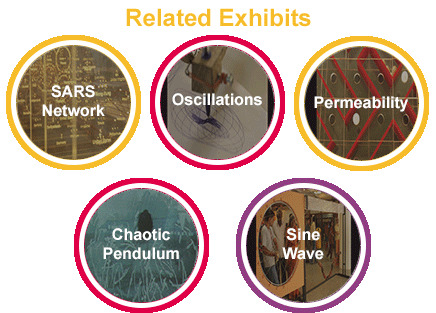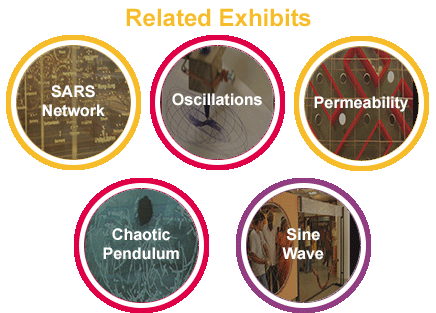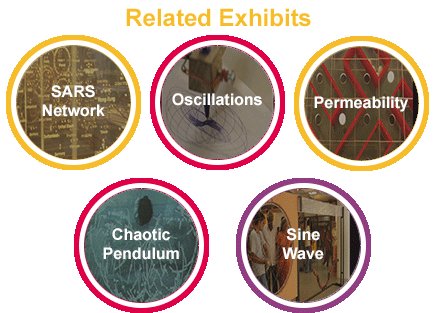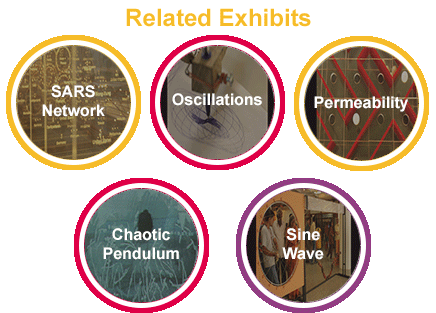
All exhibits in the Mathematics of Planet Earth - 2013 are related to each other - either directly or indirectly. The complete exhibition can be represented in the form of a network graph given below. For more information read about it at the "Adjacency Matrix" Page.